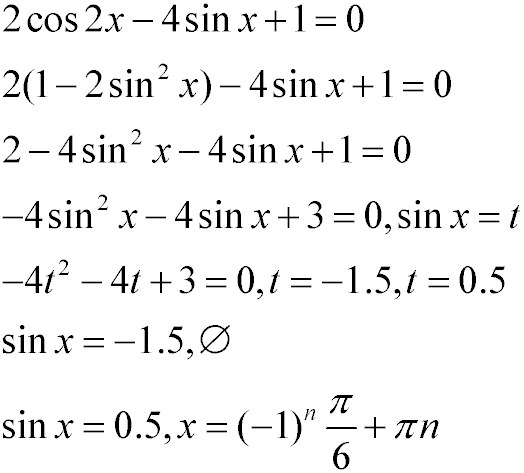Решите уравнение 2cos 2x + 4cos (3п/2 - x) + 1 = 0..

Задание:

а) решите уравнение 2cos 2x + 4cos (3п/2 - x) + 1 = 0

б) Найдите все корни этого уравнения, принадлежащие промежутку [ п ; 3п ]

Ответ:  а)  x =  (-1)ⁿ + П/6 + Пn
                б) 11п\6 ; 17п\6

Решение:

* cos (3п/2 - x) = -sin x   - Формулы приведения..
* cos 2x = cos² x - sin² x  - двойной угол.
Перепишем уравнение: 
 
* 2(cos² x - sin² x) - 4sin x + 1 = 0
* 2cos² x - 2sin² x - 4sinx + 1 =0
*cos² x = 1 - sin²x
* 2(1 - sin² x) - 2sin² x - 4sinx + 1 =0
* 2 -  2sin² x - 2sin² x - 4sinx + 1 =0
* -4sin² x - 4sin x + 3 = 0
* 4sin² x + 4sin x - 3 = 0
* Сделаем замену sin x = t
* 4t² + 4t - 3 = 0
* D = b² - 4ac = 16 + 48 = 64
* t1 = -1.5
* t2 = 1/2
* Делаем обратную замену:
  sin x = -1.5 - корней нет, так как синус - число в промежутке [-1;1];
  sin x = 1/2
   x = (-1)^{n  *}  arcsin1/2 + Пn, n Є Z
   x = (-1)ⁿ * П/6 + Пn

Другой тип решения задания: