В правильной четырехугольной пирамиде SABCD..

Задание:

В правильной четырехугольной пирамиде SABCD точка O - центр основания, S - вершина. SA = 13, BD = 10. Найдите длину отрезка SO.

Решение:

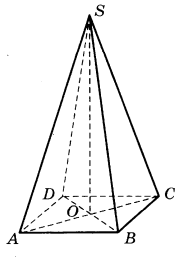
Нам нужно найти длину SO, другими словами, найти высоту пирамиды.

* Рассмотрим треугольник ASO (прямоугольный, угол O = 90°)
  SA = 13 - по условию.
  AS² = SO² + OA² - Теорема Пифагора, отсюда:
  SO² = AS² - OA²
  SO² = 13² - OA²

* AC = BD - диагонали квадрата, так как пирамида четырехугольная и правильная, значит в основании квадрат, а следовательно:
   OA = OC = OB = OD = 1/2 * BD - так как O - середина основания, значит
    OA = 1/2 * 10 = 5

*  SO² = 13² - OA²
    SO² = 13² - 5²
    SO² = 169 - 25
    SO² = 144
    SO = 12

Ответ: 12