В правильной четырёхугольной пирамиде высота..

Задание:

В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.

Решение:

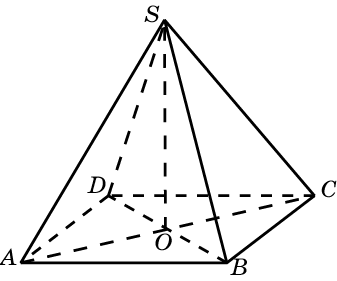
Дано:
AS  = BS = SC = DS = 5.
SO = 2

Найти: V(объем)

* V = 1/3 S_осн * h, где S_осн - Площадь основания, h = SO = высота.
* V = 1/3 Sосн * 2
* Так как пирамида правильная, значит в основании лежит квадрат. Площадь квадрата равна произведению длины на ширину, так как у квадрата все стороны равны, то площадь равна стороне в квадрате.
* Рассмотрим треугольник SOA (∠A = 90º)
 AS² = SO² + OA²
  5² = 2² + OA²
  25 = 4 + OA²
  OA² = 25 - 4
  OA² = 21
  OA = √21

* OA = R = √21 - радиус описанной окружности.
* a₄ = √2 * R - формула правильного многоугольника, где a₄ - сторона квадрата.
* a₄ = √2 * √21 = √42
* Площадь основания = площади квадрата = a₄² = (√42)² = 42

* Объем пирамиды = 1/3 * 42 * 2 = 28 (ед)³

Ответ: 28