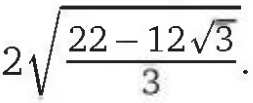Катет прямоугольного треугольника равен 2, а противолежащий...

Задание:

Катет прямоугольного треугольника равен 2, а противолежащий ему угол равен 30+ Найдите расстояние между центрами окружностей, вписанных в треугольники, на которые данный треугольник делится медианой, проведённой из вершины прямого угла.

Решение:

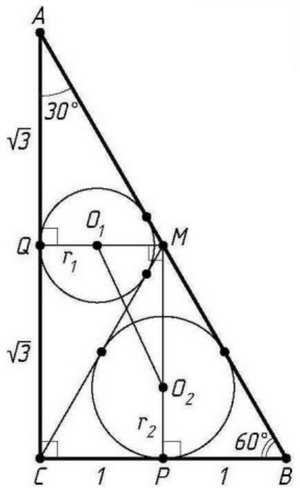
Пусть М — середина гипотенузы АВ прямоугольного треугольника АВС, ∠А = 30°, ВС = 2, O₁ и O₂ — центры окружностей, вписанных в треугольники АМС и ВМС соответственно, r₁ и r₂— радиусы этих окружностей. Тогда

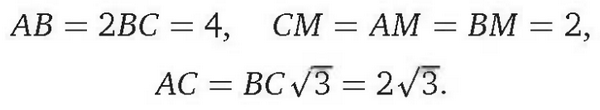
Треугольник ВСМ равносторонний, поэтому точка Р касания его вписанной окружности со стороной ВС — середина ВС, МР — средняя линия треугольника АВС,

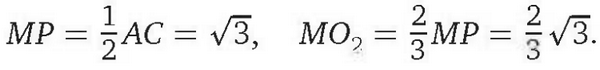
Треугольник АСМ равнобедренный, поэтому точка Q касания его вписанной окружности со стороной АС — середина AC, MQ — средняя линия треугольника АВС,

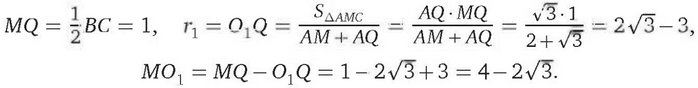
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому MO₁ и MO₂— биссектрисы смежных углов АМС и ВМС, следовательно, ∠O₁МО₂ = 90°, значит, О₁О₂ — гипотенуза прямоугольного треугольника О₁МО₂. По теореме Пифагора находим, что

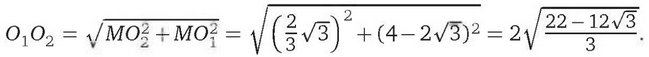
Ответ: