Медиана прямоугольного треугольника, проведённая к гипотенузе...

Задание:

Медиана прямоугольного треугольника, проведённая к гипотенузе, разбивает его на два треугольника с периметрами 8 и 9. Найдите стороны треугольника.

Решение:

Обозначим через a и b (a < b) катеты треугольника. Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, а две стороны треугольника с периметром 8 соответственно равны двум сторонам треугольника с периметром 9, разность периметров равна разности третьих сторон.
Значит,  b - а = 9 - 8 = 1. Гипотенуза данного прямоугольного треугольника равна удвоенной медиане, т. е. сумме двух сторон треугольника с периметром 8, поэтому гипотенуза равна 8 - а.

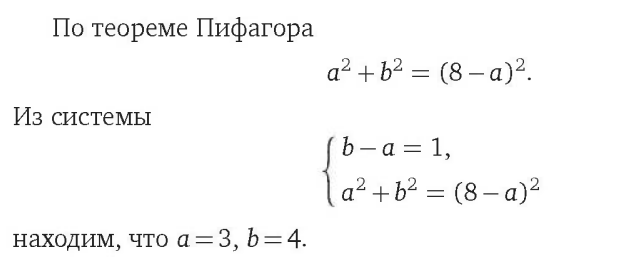
Ответ: 3; 4; 5.