Найдите трехзначное число, сумма цифр которого равна 20...
Задание:
Найдите трехзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
Решение:
Условимся, что "число А делится на число Б", "А ⋮ Б", "А mod Б = 0" означают ровно одно и то же – число А делится на число Б нацело, без остатка.
Пусть теперь x, y, z – цифры нашего числа, причем ни одна из этих цифр не равна нулю и единице, иначе суммы 20 просто не собрать.
Как же нам задавать качественные вопросы к цифрам, чтобы и не долго возиться, и перебрать все варианты?
1. Пусть все цифры делятся на 3.
x ⋮ 3, y ⋮ 3, z ⋮ 3.
В таком случае их сумма также делится на 3, но 20 не делится на 3, значит этот случай нам не подходит.
2. Пусть теперь только одна из цифр делится на 3.
x ⋮ 3, y mod 3 ≠ 0, z mod 3 ≠ 0.
В этом случае х может равняться 3, 6 или 9. Тогда имеются варианты
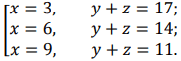
Рассматривая первую пару равенств совокупности, заключаем, что одна из цифр должна быть больше 7, чтобы другая была меньше 10. Вариантов немного – 8 или 9. Но если одна из цифр равна 8, то другая 9 и 9 делится на 3, что противоречит заданному условию.
Рассматривая вторую пару равенств совокупности, понимаем, что одна из цифр должна быть больше 4, чтобы другая была меньше 10. Варианты: одна 5, другая 9 – не подходит; одна 6 – не подходит; обе цифры равны 7. Проверяем 677: 36 + 2 ∙ 49 = 134, не подходит, не делится на 3.
Рассматривая третью пару равенств совокупности, видим, что одна из цифр должна быть больше 2, чтобы другая была меньше 10. Варианты: одна 2, другая 9 – не подходит; одна 3 – не подходит; одна 4, другая 7 – проверяем 947: 81 + 16 + 49 = 146, тоже не подходит; одна 5, другая 6 – не подходит
3. Пусть теперь две цифры из трех делятся на 3.
x ⋮ 3, y ⋮ 3, z mod 3 ≠ 0.
Квадрат последней цифры на 3 не делится. Сумма чисел, в которой все слагаемые делятся на какое-то число, кроме одного, не делится на это число. Такой случай нам не подходит.
4. Пусть ни одна из цифр не делится на 3. {x, y, z} mod 3 ≠ 0. Составим следующую таблицу
| Варианты значений | |||||
| x | 2 | 4 | 5 | 7 | 8 |
| y + z | 18 | 16 | 15 | 13 | 12 |
| y | 9 - плохо | 8; 9–плохо | 7; 6–плохо | 8; 9–плохо | 7; 4 остальное плохо |
| z | 9 - плохо | 8; 7–плохо | 8; 9–плохо | 5; 6–плохо 4–плохо | 5; 8 остальное плохо |
Проверяем 488: 16 + 64 + 64 = 144, не подходит, потому что делится на 3, а вместе с тем еще и на 9; 578: 25 + 49 + 64 = 138, подходит, делится на 3, но не делится на 9.
Надо понимать, что перестановка цифр не повлечет никаких последствий, а лишь увеличит количество подходящих и равноценных ответов: 578, 875, 758...
Ответ: 578