Найдите трехзначное число, сумма цифр которого равна 20, а сумма...

Задание:

Найдите трехзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.

Решение:

Пусть x, y и (20 – (x + y)) – цифры нашего числа, причем ни одна из них не равна 0 или 1 (иначе суммы 20 не получить) и должно выполняться условие x + y > 10.
Тогда сумма квадратов цифр запишется так:

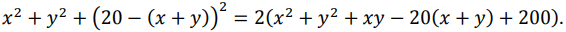
Делимость этого числа на 3 или 9 никак не зависит от чётного множителя, на него можно сократить. Теперь будем рассматривать число

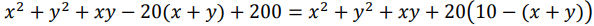
Если x и у делятся на 3, то, очевидно, первые 4 слагаемых будут делиться на 3, а 200 не делится на 3 и значит вся сумма не делится на 3.
Пусть теперь только одна из цифр делится на 3. Тогда, с учётом x + y > 10, возможны следующие пары: (3, 8), (6, 5), (6, 7), (6, 8), (9, 2), (9, 4), (9, 5), (9, 7), (9, 8). Среди этих вариантов достаточно попробовать первые 6 пар, потому что следующие будут давать уже встречавшиеся тройки цифр:

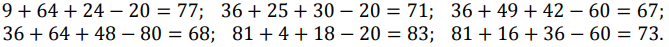
Ни одна подстановка не подходит.
Пусть, наконец, ни одна из цифр х и у не делится на 3. Пары: (4, 7), (5, 7), (5, 8), (7, 8). Достаточно попробовать первые две.

16 + 49 + 28 − 20 = 73; 25 + 49 + 35 − 40 = 69.

Последняя подстановка подходит, значит цифры могут быть такими: 5, 7, 8. Естественно, любой другой их порядок подходит: 587, 758, 785, 857, 875.

Ответ: 578