Около конуса описана сфера (сфера содержит окружность...

Задание:

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 9√2. Найдите радиус сферы.

Решение:

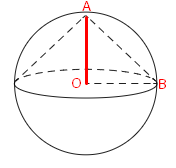
Дано:
- Конус, около которого описана сфера.
- Центр сферы совпадает с центром основания конуса.
- Образующая конуса l = 9√2.
Найти: радиус сферы R.

Решение:
1. Пусть O — центр основания конуса (и центр сферы).
   Вершина конуса — точка A, точка на окружности основания — B.
   Тогда AB = l = 9√2 — образующая.

2. Так как центр сферы находится в точке O, то:
   OA = R (расстояние от центра сферы до вершины конуса),
   OB = R (расстояние от центра сферы до точки на окружности основания).

3. Рассмотрим треугольник AOB:
   - OA = R,
   - OB = R,
   - AB = l = 9√2,
   - ∠AOB = 90° (так как вершина A и точка B на окружности основания симметричны относительно центра O, и AB — образующая).

4. По теореме Пифагора для прямоугольного треугольника AOB:
   AB² = OA² + OB²
   (9√2)² = R² + R²
   81 * 2 = 2R²
   162 = 2R²
   R² = 81
   R = 9.

Ответ: 9.