Окружность, построенная на катете прямоугольного треугольника...

Задание:

Окружность, построенная на катете прямоугольного треугольника как на диаметре, делит гипотенузу в отношении 1:3. Найдите острые углы треугольника.

Решение:

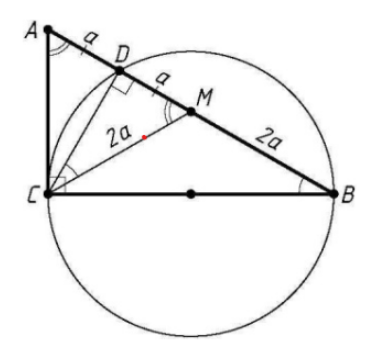
Пусть окружность, построенная как на диаметре на катете BC прямоугольного треугольника ABC, пересекает гипотенузу AB в точке D, отличной от В, причём AD = a, BD = 3a. Проведём медиану CM. Тогда AM = СМ = 2а, а так как точка D лежит на окружности с диаметром ВС, то ∠СОВ= 90°.

В прямоугольном треугольнике CDM гипотенуза СМ, равная 2а, вдвое больше катета DM:

DM = AM - AD = 2a - a = a.

Поэтому ∠DCM = 30°, a ∠АМС = 60°. Угол при вершине M равнобедренного треугольника АМС равен 60°. Следовательно, треугольник АМС равносторонний. Поэтому

∠ВАС = 60°, ∠АВС = 90° - ∠ВАС = 30°.

Ответ: 30°, 60°.