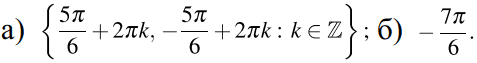Решите уравнение 2 * sin^2 x + 4 = 3√3 * sin(3π/2 + x)...
Категория: Задание 13 ЕГЭ по математике (Уравнения)
Задание:
а) Решите уравнение 2 * sin2 x + 4 = 3√3 * sin(3π/2 + x)
б) Укажите корни этого уравнения, принадлежащие отрезку [-5π/2 ; -π]
Решение:
а) Запишем исходное уравнение в виде:
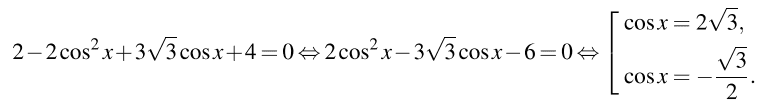
Уравнение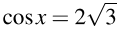 
корней не имеет. Значит, 
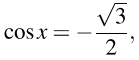откуда
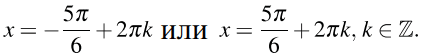
б)
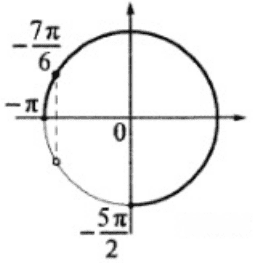
С помощью числовой окружности отберём корни, принадлежащие отрезку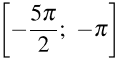 
. Получим число 
.
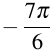Ответ: 