Точка D — середина гипотенузы АВ прямоугольного треугольника...

Задание:

Точка D — середина гипотенузы АВ прямоугольного треугольника АВС. Окружность, вписанная в треугольник ACD, касается отрезка CD в его середине. Найдите острые углы треугольника АВС.

Решение:

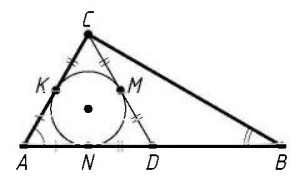
Пусть указанная окружность касается отрезка CD в его середине М, а отрезков AD и АС — в точках N иК соответственно. Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, то AD = CD. По свойству касательных, проведённых к окружности из одной точки

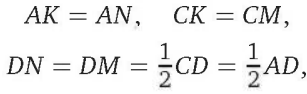
Поэтому AN = 1/2AD. Значит:

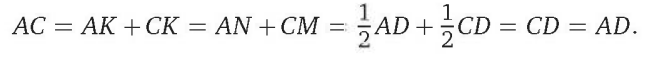
Поэтому треугольник ACD равносторонний. Следовательно,

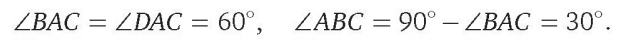
Ответ: 30°, 60°