Точка O  - центр окружности, на которой лежат точки A, B и C...

Задание:

Точка O  - центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 75º и ∠OAB = 43º. Найдите угол BCO. Ответ дайте в градусах.

Решение:

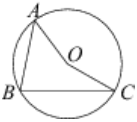
Треугольники AOB и BOC - равнобедренные, так как AO = BO = CO – радиусы окружности.
Следовательно, ∠OBA = ∠OAB=43° тогда ∠OBC = ∠ABC- ∠OBA = 75° - 43° = 32°.
По свойству равнобедренного треугольника ∠BCO=∠OBC=32°.

Ответ: 32