В параллелограмме ABCD точка Е – середина стороны АВ...

Задание:

В параллелограмме ABCD точка Е – середина стороны АВ. Известно, что EC = ED. Докажите, что данный параллелограмм – прямоугольник.

Доказательство:

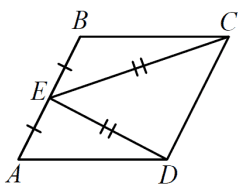
Параллелограмм отличается от прямоугольника равенством диагоналей, например. Про диагонали ничего не сообщается, значит используем другое отличие: в прямоугольнике все углы равны 90°, а в параллелограмме углы с общей стороной в сумме образуют 180°.

Треугольники ВЕС и AED равны по трем сторонам. Значит равны и соответствующие углы: ∠CBE = ∠DAE. По свойству параллелограмма, сумма этих углов равна 180°, значит каждый из них равен по 90°. Такой параллелограмм действительно прямоугольник. Что и требовалось доказать.