В прямоугольном треугольнике АВС катеты АВ и АС равны 4 и 3...

Задание:

В прямоугольном треугольнике АВС катеты АВ и АС равны 4 и 3 соответственно. Точка D делит гипотенузу ВС пополам. Найдите расстояние между центрами окружностей, вписанных в треугольники ADC и ABD.

Решение:

Пусть О₁ и О₂ — центры окружностей, вписанных в треугольники ADC и ABD соответственно, Р и Q — их точки касания со стороной ВС. Обозначим ∠ADB = α.

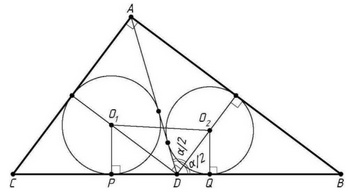
Из равнобедренного треугольника ADB находим, что

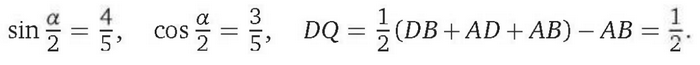
Аналогично находим, что DP = 1. Тогда

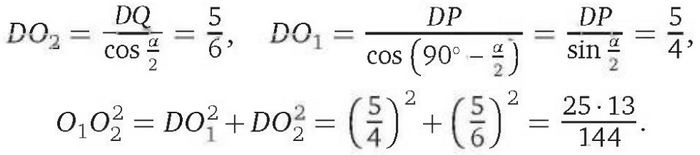
Следовательно,

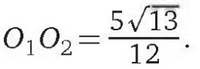
Ответ: