В равнобедренном треугольнике ABC медиана BM, проведённая к...

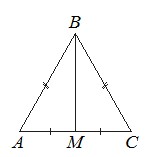
В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.

Решение:

Рассмотрим треугольник ABM: угол AMB – прямой (так как треугольник равнобедренный, и его медиана является также и высотой), BM = 12, tgA=12/5. Найдем катет треугольника через тангенс угла:

tgA = BM / AM => AM = BM / tgA = 12 / (12/5) = 5.

И вычислим гипотенузу треугольника:

AB² = AM² + BM² = 5² + 12² = 25 + 144 = 169
AB = 13

Ответ: 13