Высота прямоугольного треугольника, проведённая из вершины...

Задание:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, равна а и образует угол α с медианой, проведённой из той же вершины. Найдите катеты треугольника.

Решение:

Пусть СН = а — высота прямоугольного треугольника АВС, проведённая из вершины С прямого угла, СМ — медиана этого треугольника, причём /МСН = α.

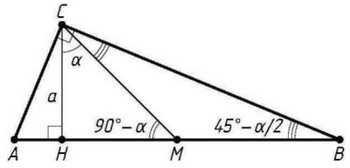
Предположим, что ВС > АС. Тогда точка М лежит между В и H. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, поэтому ВМ = AM = СМ. Угол CMH — внешний угол равнобедренного треугольника СМВ, значит,

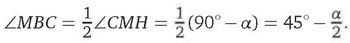
Следовательно,

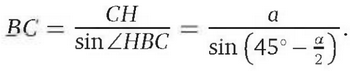
Аналогично находим, что

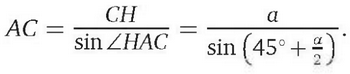
Ответ: