В основании пирамиды ABCD лежит правильный треу...

Задание:

В основании пирамиды ABCD лежит правильный треугольник АВС. Все боковые рёбра наклонены к основанию под одним и тем же углом.

а) Докажите, что АВ ⊥ CD.

б) Найдите расстояние между прямыми АВ и CD, если АВ = 8√3, AD = 5√3.

Решение:

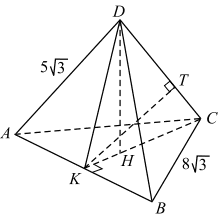
а) Рассмотрим рисунок. Так как все боковые рёбра наклонены под одним и тем же углом к основанию, то основание высоты пирамиды (на рис. это точка H) является центром окружности,

описанной около треугольника ABC. Но треугольник ABC — правильный, поэтому H является точкой пересечения высот (а значит, и медиан). Отсюда следует, что AB ⊥ CK. По условию боковые рёбра пирамиды равны, поэтому треугольник ABD равнобедренный, DK является его медианой, значит, и высотой. Значит, AB ⊥ DK. Получаем, что AB перпендикулярна двум пересекающимся прямым, лежащим в плоскости KDC, поэтому AB ⊥ KDC. Следовательно, AB ⊥ CD.

б) Проведём в треугольнике KDC высоту KT. Так как AB ⊥ KDC, то AB ⊥ KT. Значит, KT является общим перпендикуляром к прямым AB и CD, а длина отрезка KT является расстоянием между прямыми AB и CD.

В равностороннем треугольнике ABC высота KC = AC * cos 30◦ = 8√3 * √3/2 = 12, KH = 1/3*KC = 4. В треугольнике ADK AK = 1/2*AB = 4√3,

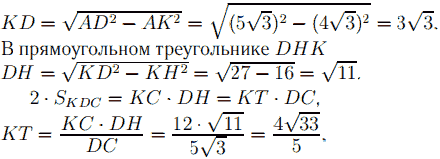
Ответ: 4√33 /5.