В правильной четырёхугольной призме ABCDA1B1C1D1...

Задание:

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ на ребре СС₁ взята точка К так, что СК : КС₁ = 1 : 2.

а) Постройте сечение призмы плоскостью, проходящей через точки D и К параллельно диагонали основания АС.

б) Найдите угол между плоскостью сечения и плоскостью основания, если CC₁ = 4,5√2, АВ = 3.

Решение:

а) Так как призма ABCDA₁B₁C₁D₁ правильная, то ABCD — квадрат и боковые грани — равные прямоугольники.

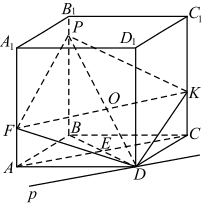
Построим сечение призмы плоскостью, проходящей через точки D и K параллельно AC. Линия пересечения плоскости сечения и плоскости AA₁C₁ проходит через точку K и параллельна AC.

В плоскости ACC₁ через точку K проведём отрезок KF параллельно диагонали AC.

Так как грани A₁ADD₁ и B₁BCC₁ призмы параллельны, то по свойству параллельных плоскостей линии пересечения плоскости сечения и этих граней параллельны. Проведём PK || FD. Четырёхугольник FPKD — искомое сечение.

б) Найдём угол между плоскостью сечения и плоскостью основания. Пусть плоскость сечения пересекает плоскость основания по некоторой прямой p, проходящей через точку D. AC || FK, следовательно, AC || p (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна этой прямой). Так как диагонали квадрата взаимно перпендикулярны, то BD ⊥ AC, а значит,
BD ⊥ p. BD — проекция PD на плоскость ABC, поэтому PD ⊥ p по теореме о трёх перпендикулярах. Следовательно, ∠PDB — линейный угол двугранного угла между плоскостью сечения и плоскостью основания.

FK || p, значит, FK ⊥ PD. В четырёхугольнике FPKD имеем FD || PK и KD || FP, значит, FPKD — параллелограмм, а так как прямоугольные треугольники FAD и KCD равны по двум катетам (AD = DC как стороны квадрата, FA = KC как расстояния между параллельными прямыми AC и F K), то FPKD — ромб. Отсюда PD = 2OD.

По условию CK : KC₁ = 1 : 2, тогда KC = 1/3*CC₁ = 4,5√2 / 3 = 1,5√2.

В ΔDKC по теореме Пифагора KD² = DC² + KC² , KD =  =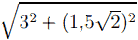
√13,5.

AC = 3√2 как диагональ квадрата, OK = EC = 1/2*AC, OK = 1,5√2.

В ΔKOD по теореме Пифагора OD² = KD² − OK²,

OD = 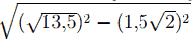 = 3. PD = 2OD = 6. 

В прямоугольном треугольнике PDB cos ∠PDB = BD / PD = 3√2 / 6 = √2 / 2 , следовательно, ∠PDB = 45◦ .

Ответ: 45◦ .