1 июня 2013 года Всеволод Ярославович...

Задание:

1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платеж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?

Решение:

Надо понять простую истину – чем больше будет платеж по кредиту, тем меньше будет долг. Меньше будет долг – быстрее его выплатишь. Максимальный ежемесячный платеж, который может себе позволить Всеволод Ярославович, равен 300 000 рублей согласно условию. Если Всеволод Ярославович будет платить максимальный платеж, то он быстрее всего погасит долг. Другими словами, сможет взять кредит на наименьший период времени, что и требуется условием.

1 июня 2013 года: долг 900 000.

• Прошел месяц: 1 июля 2013 года: долг (1 + 0,01)900 000 – 300 000 = 609 000.
• Прошел месяц: 1 августа 2013 года: долг (1 + 0,01)609 000 – 300 000 = 315 090.
• Прошел месяц: 1 сентября 2013 года: долг (1 + 0,01)315 090 – 300 000 = 18 240,9. Умножения на самом деле не очень сложные, да и умножать приятнее, чем делить.
• Прошел месяц: 1 октября 2013 года: долг (1 + 0,01)18 240,9 = 18 423,309<300 000, кредит погашен. Итого прошло 4 месяца.

Другое решение:

Минимизировать время выплат можно, только максимизировав сами выплаты. Решим задачу в общем виде. Пусть S – сумма (в тыс. руб.) кредита; S_n – задолженность в n – ый месяц; s_n – выплата в n – ый месяц, s_n = s (величина месячной выплаты одинакова и максимальна по предположению, кроме, быть может, последней выплаты); q – коэффициент ежемесячного повышения, q > 1. Тогда

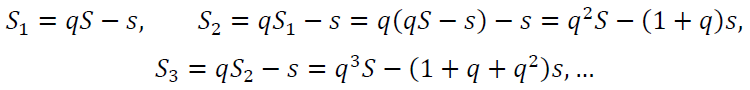
После предпоследней выплаты останется SN–1 ≤ s и тогда в последний, N – й раз, кредит будет погашен. Значит

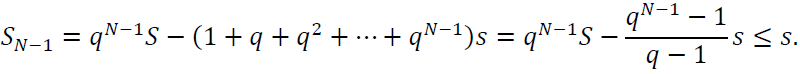Относительно x = q^N–1 получаем неравенство

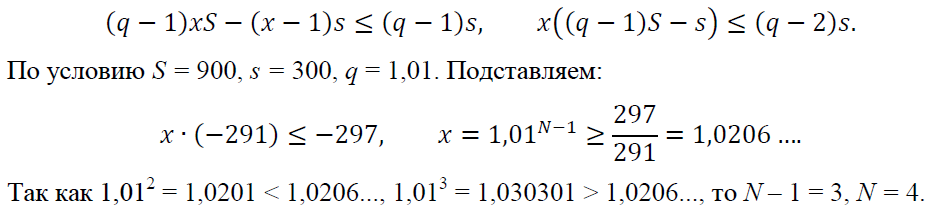
Ответ: 4 месяца.