31 декабря 2013 года Игорь взял в банке 100 000 руб...

Задание:

31 декабря 2013 года Игорь взял в банке 100 000 рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на некоторое количество процентов), затем Игорь переводит очередной транш. Игорь выплатил кредит за два транша, переведя в первый раз 51 000 рублей, во второй 66 600 рублей. Под какой процент банк выдал кредит Игорю?

Решение:

Пусть x% – искомая ставка по кредиту; m = (1 + 0,01x) – множитель оставшегося долга; a = 100 000 – сумма, взятая в банке; y₁ = 51 000, y₂ = 66 600 – размеры первого и последнего трáншей.

После первой выплаты сумма долга составит: a₁ = ma – y₁.

После второй выплаты сумма долга составит: a₂ = ma₁ – y₂ = m^₂a – my₁ – y₂. По условию, a₂ = 0. Уравнение надо будет решить сначала относительно m, выбрав подходящий корень

100000m² - 51000m - 66600 = 0,   500m² - 255m - 333 = 0.

D = 255² + 4*500*333 = 15² * 17² + 15² * 37 * 80 = 225 * (289 + 2960) = 731025.

Давайте запишем выражение для нахождения k для того, чтобы в случае вычислительной ошибки, всё же получить 2 балла по критериям.

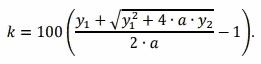
Раскладываем на множители:

731 025 / 5 = 146 205; 146 205 / 5 = 29 241; сумма цифр предыдущего числа делится на 9, значит 29 241 / 9 = 3 249; опять 3 249 / 9 = 361; ну, а 361 = 19² . Тогда 731 025 = (5 ∙ 9 ∙ 19)² = 855² . Продолжаем, выписывая только подходящий корень:

m = (255 + 855)/ 1000 = 11,1.

Тогда x = 0,11; x% = 11%.

Ответ: 11%