31 декабря 2013 года Сергей взял в банке...

Задание:

31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Решение:

Пусть сумма кредита равна a, ежегодный платеж равен x рублей, а годовые составляют k%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент m = 1 + 0,01k. После первой выплаты сумма долга составит: a₁ = am – x. После второй выплаты сумма долга составит:

a₂ = a₁m - x = (am - x)m - x = am² - xm - x = am² - (1+m)x

После третьей выплаты сумма оставшегося долга:

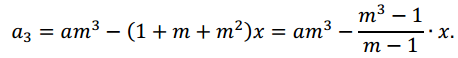
По  условию  тремя  выплатами  Сергей  должен  погасить  кредит  полностью,  поэтому:

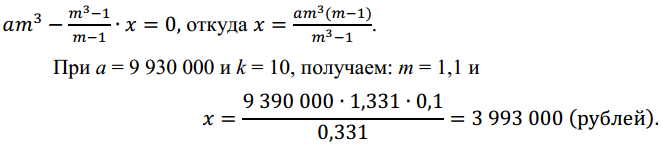
другое решение

Пусть F = 9 930 000 – величина кредита, x – искомая величина ежегодного платежа.

Первый год:

• долг: 1,1F;
• платеж: x;
• остаток: 1,1F - x.

Второй год:

• долг: 1,1(1,1F - x);
• платеж: x;
• остаток: 1,1(1,1F - x) - x

Третий год:

• долг: 1,1(1,1(1,1F - x) - x);
• платеж: x;
• остаток: 0, потому что по условию было всего три платежа..

Единственное уравнение

1,1(1,1(1,1F - x) - x) - x = 0
1,331F = 3,31x
x = 3993000

Ответ: 3993000