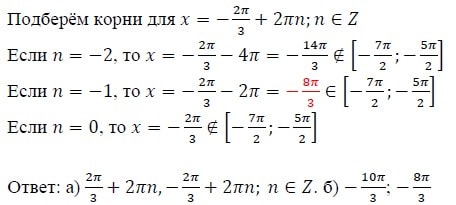а) Решите уравнение 6sin^2(x) + 7cos x - 1 = 0
Категория: Задание 13 ЕГЭ по математике (Уравнения)
Задание:
а) Решите уравнение 6sin2x + 7cos x - 1 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку [-7π/2; -5π/2]
Решение:
Основное тригонометрическое тождество
sin2x + cos2x = 1, следовательно sin2x = 1 - cos2x, подставим:
6 ∙ (1 - cos2x) + 7cos x - 1 = 0
6 - 6cos2x + 7cos x - 1 = 0
-6cos2x + 7cos x + 5 = 0;
Сделаем замену cos x = t, тогда
-6t2 + 7t + 5 = 0
D = b2 - 4ac = 49 + 120 = 169