а) Решите уравнение: cos2 х + cos2 π/6 = cos2 2х + sin...

Задание:

а) Решите уравнение: cos² х + cos² π/6 = cos² 2х + sin² π/3.

б) Укажите все корни, принадлежащие промежутку [7π/2; 9π/2].

Решение:

Так как sin π/3 = cos π/6 , то sin² π/3 = cos² π/6 , значит, заданное уравнение равно- сильно уравнению cos² x = cos² 2x, которое, в свою очередь, равносильно уравнению cos² x − cos² 2x = 0.

Но cos² x − cos² 2x = (cos x − cos 2x) * (cos x + cos 2x) и

cos 2x = 2*cos² x − 1, поэтому уравнение примет вид

(cos x − (2 cos² x − 1)) * (cos x + (2 cos² x − 1)) = 0,

(2 cos² x − cos x − 1) * (2 cos² x + cos x − 1) = 0.

Тогда либо 2 cos² x − cos x − 1 = 0, либо 2 cos² x + cos x − 1 = 0.

Решая первое уравнение как квадратное уравнение относительно cos x, получаем: (cos x)_1,2 = (1 ± √9) / 4 = (1 ± 3) / . Поэтому либо cos x = 1, либо cos x = − 1/2 . Если cos x = 1, то x = 2kπ, k ∈ Z. Если cos x = − 1/2 , то x = ± 2π/3 + 2sπ, s ∈ Z.

Аналогично, решая второе уравнение, получаем либо cos x = −1, либо cos x = 1/2 . Если cos x = −1, то корни x = π + 2mπ, m ∈ Z. Если cos x = 1/2 , то x = ± π/3 + 2nπ, n ∈ Z. Объединим полученные решения: x = mπ, m ∈ Z; x = ± π/3 +sπ, s ∈ Z.

б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.

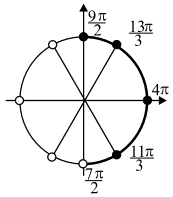
Получим: x₁ = 11π/3, x₂ = 4π, x₃ = 13π/3.

Ответ: а) mπ, m ∈ Z; ± π/3 + sπ, s ∈ Z; б) 11π/3 , 4π, 13π/3.