а) Решите уравнение cos 2х + 3 sin х - 2 = 0. б) Най...
Категория: Задание 13 ЕГЭ по математике (Уравнения)
Задание:
а) Решите уравнение cos 2х + 3sin х - 2 = 0.
б) Найдите корни уравнения, принадлежащие отрезку [-37π; -7π].
Решение:
а) cos 2x + 3 sin x − 2 = 0,
1 − 2 sin2 x + 3 sin x − 2 = 0,
2 sin2 x − 3 sin x + 1 = 0.
Пусть sin x = y, |sin x| ≤ 1, уравнение примет вид 2y2 − 3y + 1 = 0,
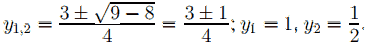
sin x = 1, x = π/2 + 2πn, n ∈ Z; sin x = 1/2 , x = (−1)k π/6 + πk, k ∈ Z;
б) Найдём корни уравнения на отрезке [−3π; −π]. С помощью числовой окружности отберём корни уравнения, принадлежащие [−3π; −π].
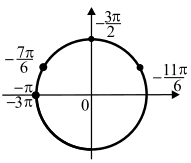
Это числа − 11π/6 , − 3π/2 , − 7π/6.
Ответ: а) π/2 + 2πn, n ∈ Z; (−1)k π/6 + πk, k ∈ Z; б) − 11π/6 , − 3π/2 , − 7π/6.