а) Решите уравнение log2^2(2 sin х + 1) - 17log2(2 sin...

Задание:

а) Решите уравнение log₂²(2 sin х + 1) - 17log₂(2 sin x + 1) + 16 = 0.

б) Укажите корни этого уравнения, принадлежащие отрезку [ π/4; 2π].

Решение:

а) После замены t = log₂(2 sin x + 1) исходное уравнение примет вид t² −17t + 16 = 0. Корни этого уравнения t = 1, t = 16. Возвращаясь к переменной x, получим:

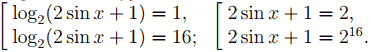
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: sin x = 1/2 , x = (−1)ⁿ *π/6 + πn, n ∈ Z.

б) Запишем решение уравнения в виде x = π/6 + 2πn, n ∈ Z или x = 5π/6 + 2πk, k ∈ Z и выясним, для каких целых значений n и k справедливы неравенства

π/4 ≤ π/6 + 2πn ≤ 2π  и  π/4 ≤ 5π/6 + 2πk ≤ 2π.

Получим: 1/24 ≤ n ≤ 11/12 и − 7/24 ≤ k ≤ 7/12, откуда следует, что нет целых значений n, удовлетворяющих неравенству 1/24 ≤ n ≤ 11/12; k = 0 — единственное целое k, удовлетворяющее неравенству − 7/24 ≤ k ≤ 7/12.

При k = 0 x = 5π/6 + 2π * 0 = 5π/6 . Итак, 5π/6 — корень уравнения, принадлежащий отрезку [π/4 ; 2π].

Ответ: а) (−1)ⁿ *π/6 + πn, n ∈ Z; б) 5π/6.