а) Решите уравнение sin 2x / sin(3π/2 + x) = 1. б) Укаж...
Категория: Задание 13 ЕГЭ по математике (Уравнения)
Задание:
а) Решите уравнение 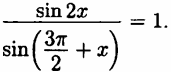 .
.
б) Укажите корни этого уравнения, принадлежащие промежутку (3π; 9π/2).
Решение:
а) 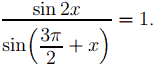
Зная, что sin 2x = 2 sin x cos x и sin (3π/2 + x) = − cos x, получим:
(2 sin x cos x) / (− cos x) = 1, где cos x ≠ 0, x ≠ π/2 + πm, m ∈ Z.
−2 sin x = 1, sin x = − 1/2.
x = − π/6 + 2πn, n ∈ Z; x = − 5π/6 + 2πk, k ∈ Z.
б) Отберём корни уравнения, принадлежащие промежутку (3π; 9π/2), с помощью числовой окружности.
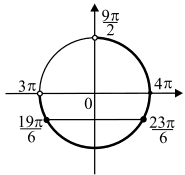
x1 = 3π + π/6 = 19π/6,
x2 = 4π − π/6 = 23π/6.
Ответ: а) − π/6 + 2πn, − 5π/6 + 2πk, n, k ∈ Z; б) 19π/6 ; 23π/6.