Часть денег от суммы 600 млн рублей размещена в...

Задание:

Часть денег от суммы 600 млн рублей размещена в банке под 14% годовых, а другая часть инвестирована в производство, причём через год эффективность вложения ожидается в размере 220% (то есть вложенная сумма х млн рублей оборачивается в капитал 2,2х млн рублей), затем отчисляются деньги на издержки, которые задаются квадратичной зависимостью 0,0031х² млн рублей. Разность между капиталом и издержками в производстве облагается налогом в 20%. Как распределить капитал между банком и производством, чтобы через год получить общую максимальную прибыль от размещения денег в банк и вложения Денег в производство? Сколько млн рублей составит эта прибыль?

Решение:

Пусть x млн рублей инвестировано в производство, тогда в банке размещено (600 − x) млн рублей.

Деньги в банке размещены под 14% годовых, поэтому через год в банке станет 1,14(600 − x) млн рублей.

По условию через год эффективность вложения в производство ожидается в размере 220%, то есть вложенные x млн рублей превратятся в 2,2x млн рублей. Теперь от 2,2x нужно вычесть деньги на издержки, которые задаются квадратичной зависимостью 0,0031x² : (2,2x − 0,0031x²) млн рублей, после чего нужно заплатить налог в 20% от этой суммы, поэтому останется 80% этой суммы, то есть 0,8 * (2,2x − 0,0031x²) млн рублей. Рассмотрим функцию прибыли

f(x) = 1,14(600 − x) + 0,8 * (2,2x − 0,0031x²) − 600,

f(x) = −0,8 * 0,0031x² + 0,62x + 84.

Это квадратичная функция, наибольшее значение она принимает в точке

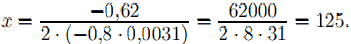
f(125) = −0,8 * 0,0031 * 125² + 0,62 * 125 + 84 = −38,75 + 77,5 + 84 = = 122,75 (млн рублей).

Итак, прибыль составит 122,75 млн рублей.

Ответ: 122,75.