Дано трехзначное натуральное число... а) Может ли...

Задание:

Дано трехзначное натуральное число (число не может начинаться с нуля).

а) Может ли частное этого числа и суммы его цифр быть равным 20?

б) Может ли частное этого числа и суммы его цифр быть равным 81?

в) Какое наименьшее натуральное значение может иметь частное данного числа и суммы его цифр?

Ответ: а)  да б)  нет в)  11

Решение:

а)  Пусть число N = 100a + 10b + c, где а,b,c — число сотен, десятков и единиц соответственно, следовательно, они могут принимать натуральные значения от 0 до 9 (только a не может быть равно 0).

Предположим, что

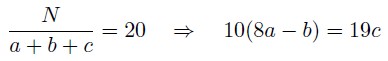
Пусть 8a = b, откуда, так как a, b - цифры, то а = 1 и b = 8. Тогда 10(8a — b) = 0, следовательно, 19c = 0, откуда c = 0. Таким образом, получили число 180.

Проверкой убеждаемся, что действительно 180 : (1 + 8 + 0) = 20.

Ответ: да.

б) Предположим, что

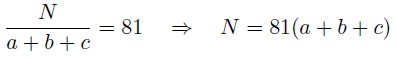
Следовательно, N делится на 81, следовательно, его можно представить в виде N = 81 * к, где к -некоторое натуральное число и k = a + b + c. Заметим, что так как N - трехзначное число, то 81 * к <= 999, откуда к <= 12.

Из того, что N делится на 81, можно сделать вывод, что N делится на 9. Следовательно, сумма его цифр должна делиться на 9. Но так как сумма его цифр равна k, а k < 12, то k = 9. Следовательно, N = 9 * 81 = 729. Но у числа 729 сумма цифр не равна 9, следовательно, 729 не подходит. Так как это был единственный возможной вариант, то ответ: нет.

в) Рассмотрим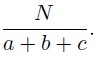  

Попробуем поискать наименьшее трехзначное число с наибольшей суммой цифр. Значит, в нем должно быть мало сотен и много десятков и единиц. Возьмем 198. Сумма его цифр равна 18 и оно нацело делится на нее, в результате чего получаем 11.

Докажем, что 11 — наименьшее натуральное частное от деления числа на сумму его цифр. 

Предположим противное. Пусть частное от деления N = 100a + 10b + сc на a + b + c равно k, оде к <= 10 натуральное число, тогда:

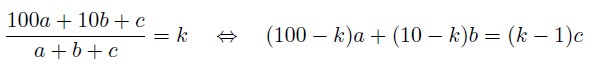
Так как число сотен не может быть равно нулю, то а >= 1. Так как к <= 10, то 100 — k >= 90, следовательно, (100 - k) * a >= 90. Так как b >= 0, то (10 - k) * b  >= 0, следовательно, вся левая часть равенства >= 90.

Так как число единиц не может быть больше 9, то есть c <= 9, и (k - 1) <= 9, то (k-1) * c  <= 9 * 9 = 81.