Катеты прямоугольного треугольника равны 15 и 36...

Задание:

Катеты прямоугольного треугольника равны 15 и 36. Найдите высоту проведенную к гипотенузе.

Решение:

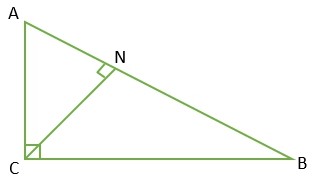
Дано:

AC = 36;
BC = 15;
Угол C = 90°

Найти: CN

Решение:

1. Площадь треугольника ABC = 1/2 * AC * BC
   Площадь треугольника ABC = 1/2 * 15 * 36 = 15 * 18 = 270

2. AB² = AC² + BC²
    AB² = 36² + 15²
    AB² = 1296 + 225 = 1521
    AB = √1521 = 39

3. Чтобы найти высоту CN, используем другую формулу площади прямоугольного треугольника, а именно: S = 1/2 * a * h, где S - площадь треугольника, a - гипотенуза AB, h - высота CN.
Из формулы выразим h, и получим, что:
  h = 2S/a
  CN = 2S/AB
  CN = 2 * 270/39 = 540/39, примерно 13.8

Ответ: 13.8