На доске написали несколько не обязательно различных...

На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 330. В каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).

а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.

б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?

в) Найдите наибольшее возможное значение суммы получившихся чисел.

Ответ:

а) 14 x 19 + 64, где запись 14 x 19 означат сумму из 14 слагаемых, каждое из которых равно 19

б)  Нет

в) 1518

Решение:

Пусть i-ое выписанное число имеет вид:

 

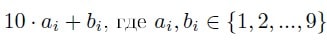
Для суммы b_i по всем значениям индекса i, таким, что слагаемое b_i есть этой в сумме, используем обозначение 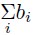. Тогда сумма всех исходных чисел имеет вид:

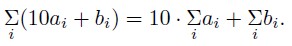
Обозначим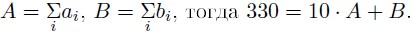  
После смены мест цифр i - oe получение число имеет вид: 10 x b_i + a_i. Тогда сумма всех полученных чисел имеет вид:

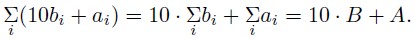
а) Увеличение суммы в 4 раза равносильно тому, что новая сумма равна 330 * 4 = 1320, что равносильно 10 * B + A = 1320. Рассмотрим систему:

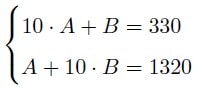
вычитая из второго уравнения первое, находим, что 9 * B - 9 * A = 990, откуда B = 110 + A. Подставляя это в первое уравнение системы, находим A = 20, тог да B = 130.
Попробуем брать в качестве b_i 9, пока их сумма не превосходит 130 - так можно положить

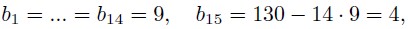
то есть в сумме 15 слагаемых. Тогда можно положить

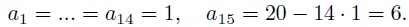
б) Увеличение суммы в 2 раза равносильно тому, что новая сумма равна 330 * 2 = 660, что равносильно 10 * B + A = 660. Рассмотрим систему:

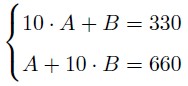
вычитая из второго уравнения первое, находим, что 9 * B - 9 * A = 330, но 330 те делится на 9, следовательно, такой случай не возможен.

в) Пусть сумма полученных чисел равна S, что равносильно системе 

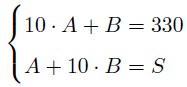
вычитая из второго уравнения первое, находим, что

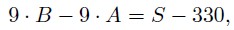
откуда

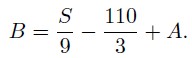
Подставляя это в первое уравнение системы, находим

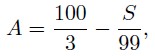
откуда в частности следует, что

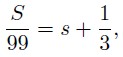
то есть S = 99s + 33 для некоторого целого неотрицательного s, тогда A = 33 — s, B = 10s.
Покажем, что B < 170:
в самом деле, если бы было B ≥ 170, тогда число слагаемых в исходной сумме было бы не менее, чем 19 (так как 18 * 9 < 170), но тогда

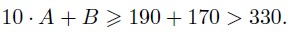
Так как B < 170, то 10s < 170, то есть s ≤ 16.
При s = 16 получим A = 17, B = 160, но даже 17 * 9 = 153 < B, а количество чисел не может быть больше, чем 17 (= A), следователь но, s ≤ 15.
При s = 15 получим A =18, B = 150
Аналогично примеру из пункта а) построим решение:
Попробуем брать в качестве b_i 9, пока их сумма не превосходит 150 - так можно положить:

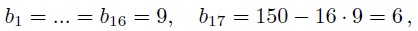
то есть в сумме 17 слагаемых. Тогда можно положить:

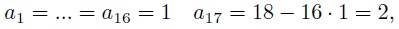
итого, искомая сумма 16 x 19 + 26, максимальная S = 99 * 15 + 33 = 1518