Найдите площадь поверхности прямой призмы, в основании...
Категория: Задание 8 ЕГЭ по математике (Стереометрия)
Задание:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 4 и 3, и боковым ребром, равным 8.
Решение:
Площадь боковой поверхности призмы находим по формуле Sбок. = Pосн. * h = 4a * h, где Pосн. и h — соответственно периметр основания и высота призмы, равная 8, и a — сторона ромба. Найдём сторону ромба, пользуясь тем, что диагонали ромба взаимно перпендикулярны и точкой пересечения делится пополам.
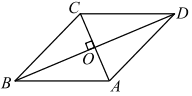
Из треугольника BOC по теореме Пифагора находим BC2 = BO2 + OC2 = (4/2)2 + (3/2)2 = 4 + 2,25 = 6,25, BC = 2,5. Следовательно, Sбок. = 4 * 2,5 * 8 = 80. Sосн. = 1/2 * AC * BD = 1/2 * 4 * 3 = 6. Отсюда, Sпов. призмы = 2Sосн. + Sбок. = 2 * 6 + 80 = 92.
Ответ: 92.