Найдите все значения a.. |a^2 + 3 - x| + |x - a - 2|...

Задание:

Найдите все значения a, при каждом из которых уравнение
|a² + 3 - x| + |x - a - 2| + |x  - 3a - 1| = a² - a + 1
имеет хотя бы один корень.

Решение:

Используем «неравенство треугольника»: |x + y| <= |x| + |y|, где равенство
достигается, если x и y или оба неотрицательны, или оба неположительны.
Поскольку a² - a + 1 > 0, будем иметь:

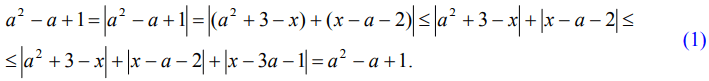
Следовательно, в цепочке (1) все неравенства обращаются в равенства. Это
возможно лишь в том случае, когда (a² + 3 - x) и (x - a - 2) неотрицательны (так как их сумма положительна), а x  - 3a - 1 = 0. Получим систему условий:

Подставим значение x = 3a + 1 из первого равенства системы (2) во второе и третье:

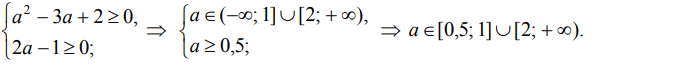
Ответ: [0,5; 1] U [2; +∞).