Найдите все значения а, при каждом из которых...

Задание:

Найдите все значения а, при каждом из которых система уравнений 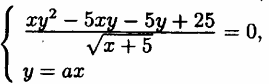 имеет ровно два различных решения.

Решение:

Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.

Первое уравнение 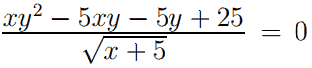 параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.

Запишем уравнение в виде 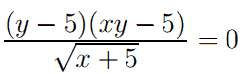, разложив числитель на множители.

При x ≤ −5 левая часть не имеет смысла. При x > −5 уравнение задаёт прямую y = 5 и гиперболу y = 5/x (см. рис.).

Найдём координаты точек A, B и C. B — точка пересечения прямой y = 5 и гиперболы y = 5/x , чтобы найти её координаты, нужно решить систему уравнений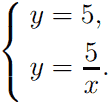  

Получаем B(1; 5).

У точек A и C абсцисса равна −5, ординаты находим из уравнений прямой и гиперболы. A(−5; 5) и C(−5; −1).

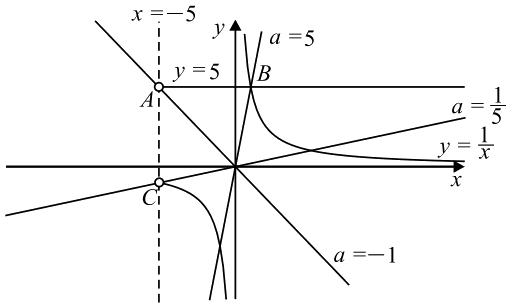
При каждом значении a уравнение y = ax задаёт прямую с угловым коэффициентом a, проходящую через начало координат. Чтобы найти значение a, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой. Например, для точки A(−5; 5) получаем x = −5, y = 5, 5 = a · (−5), a = −1. Аналогично для B(1; 5) a = 5 и для C(−5; −1) a = 1/5 .

При x > −5 прямая y = ax пересекает прямую y = 5 при a < −1 и a > 0, пересекает правую ветвь гиперболы y = 5/x при a > 0, пересекает левую ветвь гиперболы y = 5/x при a > 1 5 . При этом прямая y = ax проходит через точку пересечения прямой y = 5 и гиперболы y = 5/x при a = 5.

Число решений исходной системы равно числу точек пересечения прямой y = 5 и гиперболы y = 5/x с прямой y = ax при условии x > −5. Таким образом, исходная система имеет ровно два решения при 0 < a ≤ 0,2; a = 5.

Ответ: (0; 0,2]; {5}.