Найдите все значения параметра а,..на отрезке [3; 4]...

Задание:

Найдите все значения параметра а, при каждом из которых система неравенств 

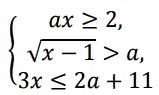
имеет хотя бы одно решение на отрезке [3; 4].

Решение:

Рассмотрим семейства следующих графиков:

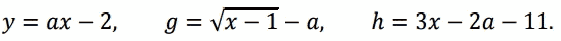
Неравенство у ≥ 0 будет выполняться хотя бы для одного х из [3; 4] в том случае, если прямая у = ах - 2 будет иметь общую точку с фигурой, ограниченной осью ܱОх и линиями х = 3, х = 4 для всех у ≥ 0. Это достигается при всех а ≥ 1/2.

Из аналогичных рассуждений для g получаем а < √3.

Неравенство h ≤ 0 будет выполняться хотя бы для одного x из [3; 4] в том случае, если прямая ݄h = 3x - 2a - 11 будет иметь общую точку с фигурой, ограниченной осью ܱОх и линиями х = 3, х = 4 для всех у ≤ 0. Это достигается при всех а ≥ -1. Пересекая полученные неравенства, получаем ответ.

Ответ: 1/2 ≤ а < √3.