Найдите все значения параметра а, при каждом...

Задание:

Найдите все значения параметра а, при каждом из которых уравнение 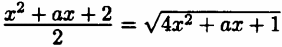 имеет ровно три различных корня.

Решение:

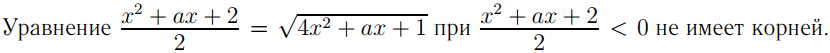
При x² + ax + 2 > 0 обе части уравнения можно возвести в квадрат.

(x² + ax + 2)² = 4(4x² + ax + 1),

x⁴ + ax³ + 2x² + ax³ + a²x² + 2ax + 2x² + 2ax + 4 = 16x² + 4ax + 4,

x⁴ + 2ax³ + x²(a² − 12) = 0,

x²(x² + 2ax + a² − 12) = 0,

x²((x + a)² − 12) = 0,

x₁ = 0, (x + a − √12)(x + a + √12) = 0,

x₂ = −a + √12, x₃ = −a − √12.

Чтобы исходное уравнение имело три различных корня, необходимо, чтобы числа x₁, x₂, x₃ были различными и для каждого из этих чисел выполнялось условие x₂+ax+2 ≥ 0.

x₂ ≠ 0 и x₃ ≠ 0, если a ≠ √12 = 2√3 и a ≠ − √12 = −2√3.

Обозначим g(x) = x² + ax + 2. g(0) = 2 > 0. Числа x₂ = −a + 2√3 и x₃ = −a − 2√3 будут корнями исходного уравнения, если выполняются условия:

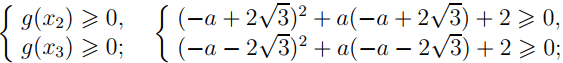
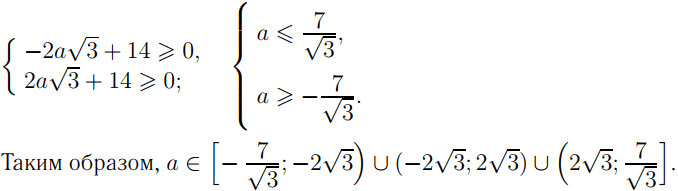
Ответ: [- 7/√3 ; - 2√3)  ( - 2√3 ; 2√3)  ( 2√3 ; 7/√3].