Найдите все значения а, при каждом из которых ур...

Задание:

Найдите все значения а, при каждом из которых уравнение 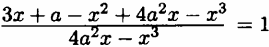 имеет единственный корень.

Решение:

В левой части уравнения выделим целую часть 

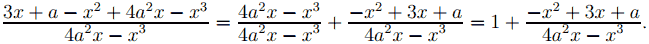Тогда уравнение примет вид  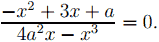Оно равносильно системе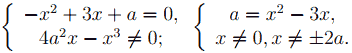  

Решим систему графически в системе координат xOa. Для этого строим графики функций a = x² − 3x и a = ± x/2 . Графиком функции a = x 2 − 3x является парабола, ветви которой направлены вверх. Вершина параболы — точка (3/2; - 9/4), точки (0; 0) и (3; 0) принадлежат параболе. Графиками функций a = ± x/2 являются прямые.

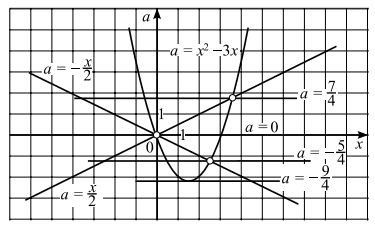
Решая уравнение x² − 3x = x/2 , находим точки пересечения прямой a = x/2 и параболы a = x² − 3x: x = 0, x = 7/2 , откуда a = 0, a = 7/4 . Аналогично, решая уравнение x² − 3x = − x/2 , находим x = 0, x = 5/2 . Тогда a = 0, a = − 5/4 . Выкалываем эти точки.

По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при a = − 9/4 , a = − 5/4 , a = 0, a = 7/4.

Ответ: − 9/4 ; − 5/4 ; 0; 7/4.