Найдите все значения параметра а, при каждом из...

Задание:

Найдите все значения параметра а, при каждом из которых система 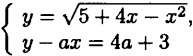 имеет ровно два решения.

Решение:

Построим график уравнения .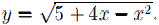

Преобразовав подкоренное выражение, получим:

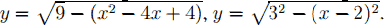
Если y ≥ 0, то y² = 3² − (x − 2)² , (x − 2)² + y² = 3².

Если y < 0, точек, удовлетворяющих уравнению, нет.

Получилась полуокружность с центром в точке (2; 0) радиусом 3, лежащая в верхней полуплоскости.

Уравнение y − ax = 4a + 3 запишем в виде y = a(x + 4) + 3 — семейство прямых с угловым коэффициентом a, проходящих через точку M(−4; 3).

Рассмотрим рисунок. Видно, что прямая и полуокружность имеют две общие точки, если a₂ ≤ a < a₁. Прямая BM касается окружности, её угловой коэффициент равен 0, значит, a₁ = 0. Найдём a₂ из условия, что прямая MC y = a(x + 4) + 3 проходит через точку C(5; 0), то есть y(5) = 0.

a(5 + 4) + 3 = 0, a = − 1/3 , значит, a₂ = − 1/3. Значит, система имеет ровно два решения при − 1/3 ≤ a < 0.

Ответ: [− 1/3 ; 0).