Найдите все значения параметра а, при которых...

Задание:

Найдите все значения параметра а, при которых уравнение 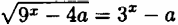 имеет единственный корень.

Решение:

Пусть 3^x = t,t > 0. Заметим, что после замены каждому положительному корню уравнения √(t² − 4a) = t − a соответствует единственный корень исходного уравнения (это следует из монотонности функции 3^x = t). Уравнение √(t² − 4a) = t − a равносильно системе

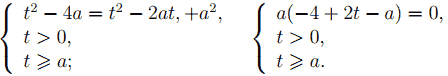
Если a = 0, то любое t > 0 является корнем первого уравнения системы, следовательно, исходное уравнение имеет бесконечное множество корней. Значит, a ≠ 0, тогда система примет вид

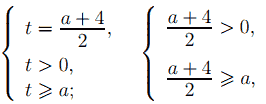
откуда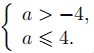 

Учитывая, что a ≠ 0, получаем: −4 < a < 0, 0 < a ≤ 4.

Ответ: (−4; 0) ∪ (0; 4].