Объем конуса равен 12. Параллельно основанию конуса...

Задание:

Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.

Решение:

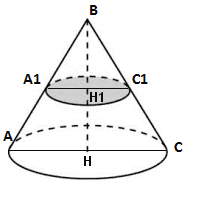
По условию задачи сечение делит высоту BH пополам, а значит отношение BH/BH₁ = 2. Отношение HC/H₁C₁ = 2.

1) Площадь конуса = 1/3 * площадь основания * на высоту конуса. Так как в основании конуса окружность, то площадь конуса S = 1/3 * π * R² * H, где R - радиус основания (то есть окружности). H - высота. π = 3.14 - константа.

2) Для большого конуса S = 1/3 * π * HC² * BH

1/3 * π * HC² * BH = 12 - по условию
π * HC² * BH = 12 * 3
π * HC² * BH = 36

3) Для меньшего конуса S = 1/3 * π * H₁C₁ * BH₁, а мы знаем, что BH₁ в 2 раза меньше BH, а H₁C₁ в 2 раза меньше HC, подставляем данные в S.

S = 1/3 * π * H₁C₁ * BH₁
S = 1/3 * π * (HC/2)² * BH/2
S = 1/3 * π * HC² / 4 * BH/2
S = 1/3 * π * HC² * BH / 8, помним, что π * HC² * BH = 36, подставляем
S = 1/3 * 36 / 8 = 12 / 8 = 1.5

Ответ: 1.5