Оля хочет взять в кредит 1 000 000 рублей. Погашение...

Задание:

Оля хочет взять в кредит 1 000 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 240 000 рублей?

Решение:

1 способ:

Первый год (сказано, что погашение происходит раз в год после начисления процентов): долг (1 + 0,1) * 1 000 000 – 240 000 = 860 000.

Второй год: долг (1 + 0,1) * 860 000 – 240 000 = 706 000.

Третий год: долг (1 + 0,1) * 706 000 – 240 000 = 536 600.

Четвертый год: долг (1 + 0,1) * 536 600 – 240 000 = 350 260.

Пятый год: долг (1 + 0,1) * 350 260 – 240 000 = 145 286.

Шестой год: долг (1 + 0,1) * 145 286 = 159 814,6 < 240 000, конец.

2 способ:

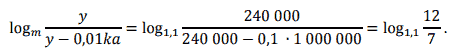
Полученное число, очевидно, не целое (аргумент логарифма не является степенью с натуральным показателем основания логарифма). Поэтому берем целую часть числа и прибавляем единичку.

Ответ: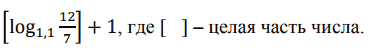 

3 способ:

Минимизировать время выплат можно, только максимизировав сами выплаты. Решим задачу в общем виде. Пусть S – сумма (в тыс. руб.) кредита; S_n – задолженность в n – ый год; s_n – выплата в n – ый год, s_n = s (величина годовой выплаты одинакова и максимальна по предположению, кроме, быть может, последней выплаты); q – коэффициент ежегодного повышения, q > 1. Тогда

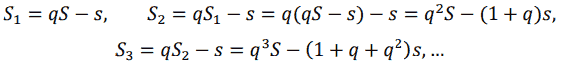
После предпоследней выплаты останется S_N–1 ≤ s и тогда в последний, N – й раз, кредит будет погашен. Значит

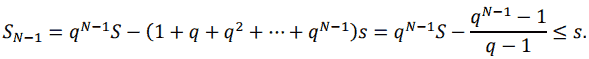
Относительно x = q ^N–1 получаем неравенство

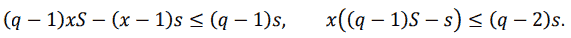
По условию S = 1000, s = 240, q = 1,1. Подставляем:

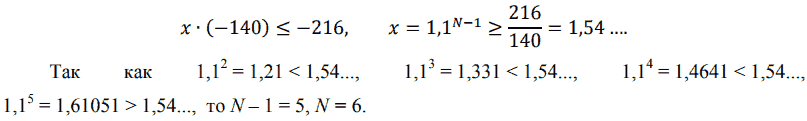
Ответ: 6 лет