Пенсионный фонд...t^2 тыс...конце года t (t = 1; 2;...)...

Задание:

Пенсионный фонд владеет ценными бумагами, которые стоят t² тыс. рублей в конце года t (t = 1; 2;...). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1 + r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?

Решение:

За год ценные бумаги увеличиваются в цене в

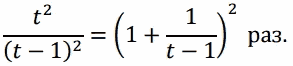
Видно, что относительное увеличение стоимости замедляется с каждым годом. Продавать бумаги и класть деньги в банк имеет смысл в том случае, когда в банке прирост за год (а, значит, и за все последующие годы) станет больше. По условию, продавать бумаги нужно в конце 21-го года, значит, за 21-ый год прирост стоимости ценных бумаг еще больше банковского процента, а в 22-м году – уже нет. Записываем:

21-ый год: 

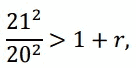
22-й год: 

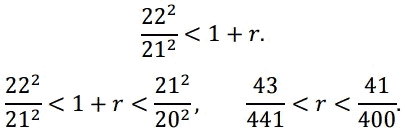
Ответ: 43/441 < r < 41/400.