При каких значениях параметра а система x - √3|y|

Задание:

При каких значениях параметра а система 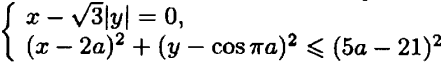 имеет ровно два решения?

Решение:

Решим задачу графически. Если |5 − 2a| = 0, то неравенство системы задаёт круг с центром в точке (2a; cos πa) и радиусом |5a − 21|. Если |5a − 21| = 0, то решением неравенства будет единственная точка: x = 2a = 42/5 , y = cos πa = cos 21π/5 , а тогда у системы не может быть более одного решения.

Уравнение системы задаёт угол, биссектрисой которого является ось Ox. Сторона этого угла проходит через точки (0; 0) и (1; 1/√3) и поэтому образует угол 30◦ с положительным направлением оси Ox.

Ровно два решения будет, если круг касается обеих сторон угла. Тогда центр круга должен лежать на биссектрисе угла, то есть на луче Ox. Следовательно, ордината центра круга должна равняться нулю, а абсцисса быть больше нуля. Ордината равна нулю, если

cos πa = 0, πa = π/2 + πk, k ∈ Z, a = 1/2 + k, k ∈ Z.

Абсцисса центра круга равна 2a и равна 2k + 1, она больше нуля, если k ≥ 0. Рассмотрим ΔO₁OM, где O₁ — центр круга, M — одна из точек касания. Тогда O₁M = |5a − 21|, OO₁ = 2a, ∠O₁MO = 90◦ , ∠MOO₁ = 30◦. Тогда

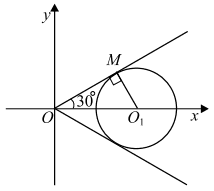
O₁M = O₁O * sin ∠O₁OM = 2a sin 30◦ = a.

Значит, a = |5a − 21|, k + 1/2 =  |5k + 5/2 − 21|, k + 1/2 = |5k − 37/2|; отсюда

либо k + 1/2 = 5k − 37/2 , то есть 4k = 19, k = 19/4 ;

либо k + 1/2 = 37/2 − 5k, 6k = 18, k = 3. k — целое число.

19/4 ∉ Z; 3 ∈ Z и 3 ≥ 0. Таким образом, k = 3, a = 1/2 + k = 3,5.

Ответ: 3,5.