Прямая, параллельная стороне AC треугольника ABC, пересекает стороны...

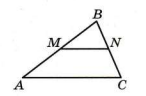
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC = 44, MN = 24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MNB.

Решение:

Рассмотрим треугольники ABC и MBN:
1) угол MBN - общий
2) угол CAB = углу NMB, так как MN || AC и эти углы являются соответственными
3) угол ACB = углу MNB, так как MN || AC и эти углы являются соответственными

Следовательно, треугольники ABC и MBN подобны.

Таким образом, площади треугольников соотносятся как квадрат оснований:

(44 : 24)² = 121 : S_MNB

S_MNB = (121 * 24²) / (44)² = 36

Ответ: 36.