В августе планируется взять кредит в банке на сумму...

Задание:

В августе планируется взять кредит в банке на сумму 3 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;

— с февраля по июль каждый год необходимо выплатить часть долга;

— в августе каждого года долг должен быть на одну и ту же сумму меньше долга на август предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 5,1 млн рублей?

Решение:

Пусть кредит планируется взять на n лет. Ежегодный платёж состоит из двух частей: одна и та же сумма x = 3/n млн рублей, на которую каждый год уменьшается сумма кредита (долга), и плата за пользование кредитом, которая составляет 20% от оставшегося долга. Долг перед банком (в млн рублей) по состоянию на май должен уменьшаться до нуля равномерно:

3; 3 − x; 3 − 2x; . . . ; 3 − (n − 1)x; 0.

Ежегодные выплаты процентов за пользованием кредитом составят (в млн рублей):

0,2 * 3; 0,2 * (3 − x); 0,2 * (3 − 2x); . . . ; 0,2 * (3 − (n − 1)x).

Сумму выплат процентов за пользование кредитом посчитаем как сумму арифметической прогрессии.

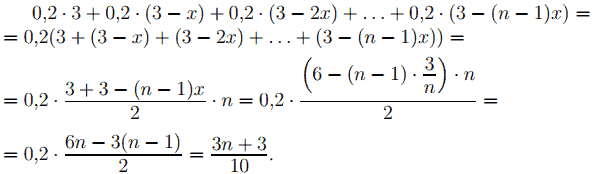
За n лет клиент банка должен выплатить 3 млн рублей кредита и проценты за пользование кредитом (3n + 3) /10 млн рублей, что по условию равно 5,1 млн рублей.

3 + (3n + 3)/10 = 5,1; (3n + 3)/10 = 2,1, 3n + 3 = 21, n = 6.

Кредит планируется взять на 6 лет.

Ответ: 6.