В двух областях есть по 50 рабочих, каждый из которых...
Задание:
В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x 2 человеко-часов труда, а для добычи y кг никеля в день требуется y 2 человеко-часов труда. Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором 1 кг алюминия приходится на 2 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение:
Пусть в первой области х рабочих заняты на добыче алюминия, а 50 − х рабочих заняты на добыче никеля, и пусть во второй области y рабочих заняты на добыче алюминия, а 50 − y рабочих заняты на добыче никеля. Внесем данные из условия в таблицу.
Для производства сплава масса добытого алюминия должна быть вдвое меньше массы добытого никеля:
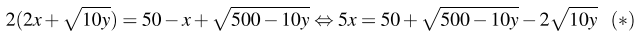
Пусть s кг — масса сплава, она равна сумме масс алюминия и никеля: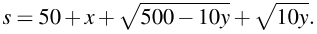 
Будем искать наибольшее возможное значение этого выражения, подставив в него (*):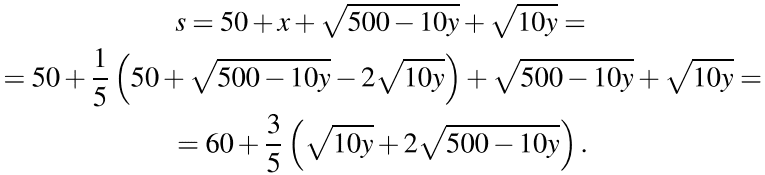 
Наибольшему возможному значению s соответствует наибольшее значение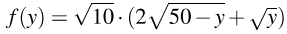 
при натуральных y не больших 50. Имеем:
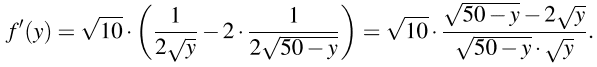
Найдем нули производной:
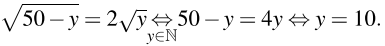
В найденной точке производная меняет знак с плюса на минус, поэтому в ней функция достигает максимума, совпадающего с наибольшим значением функции на исследуемой области.
Далее имеем: f(10) = 50, s = 60 + 30 = 90 кг, из (*) находим x = 10 чел. Это означает, что 10 рабочих первой области и 10 из второй должны быть заняты на производстве алюминия, за сутки они добудут 20 + 10 = 30 кг алюминия, оставшиеся 40 рабочих первой области и 40 рабочих второй области должны быть заняты на добыче никеля, за сутки они добудут 40 + 20 = 60 кг никеля. Из добытых металлов будет произведено 90 кг сплава.
Ответ: 90 кг.