В школах №1 и №2 учащиеся писали тест. Из каждой школы...

Задание:

В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали, по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.

а) Мог ли средний балл в школе №1 уменьшиться в 10 раз?
б) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?
в) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.

Решение:

а) Пусть в школе №1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал 19 баллов и перешел в школу №2. Тогда средний балл в школе №1 уменьшился в 10 раз.

б) Пусть в школе №2 писали тест m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов. Тогда получаем:

u = 0.9(m + 1)B -mB; 10u = (9 - m)B.

Если B = 7, то (9 − m)B не делится на 10, а 10u делится на 10. Но это невозможно, поскольку 10u = (9 − m)B.

в) Пусть в школе №1 средний балл равнялся A. Тогда получаем 

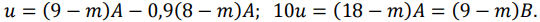
Заметим, что если B = 1 или B = 3, то 10u = (9 − m)B не делится на 10. Если B = 2 или B = 4, то m = 4. В первом случае 14A = 10, а во втором 14A = 20. Значит, один из этих случаев не возможен. При B = 5 и m = 3 получаем u = 3 и A = 2. Этот случай реализуется, например, если в школе №1 писали тест 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, в школе №2 писали тест 3 учащихся и каждый набрал по 5 баллов, а у перешедшего из одной школы в другу учащегося – 3 балла.

Ответ: а) 44; б) нет; в) 5.