В сосуд, имеющий форму правильной треугольной...
Категория: Задание 8 ЕГЭ по математике (Стереометрия)
Задание:
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 40 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в два раза больше, чем у первого? Ответ выразите в сантиметрах.
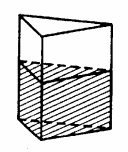
Решение:
Пусть a — сторона основания первого сосуда, тогда 2a — сторона основания второго сосуда. По условию объём жидкости V в первом и втором сосуде один и тот же. Обозначим через H уровень, на который поднялась жидкость во втором сосуде.
Тогда V = 1/2 * a2 * sin 60◦ * 40 = (a2√3)/4 * 40, и V = ((2a)2√3)/4 * H.
Отсюда (a2√3)/4 * 40 = ((2a)2√3)/4 * H, 40 = 4H, H = 10.
Ответ: 10.