Вклад планируется положить на пять лет, он состав...

Задание:

Вклад планируется положить на пять лет, он составляет целое число сотен тысяч рублей. В конце каждого года вклад увеличивается на 20% по сравнению с его размером в начале года, кроме этого, в начале четвёртого и пятого годов вклад ежегодно пополняется на 100 тысяч рублей. Найдите наибольший размер первоначального вклада, при котором через пять лет он будет меньше 800 тысяч рублей.

Решение:

Составим математическую модель задачи. Увеличение вклада на 20% означает умножение начальной суммы на 1,2. Пусть первоначальный вклад равен P сотен тысяч рублей. Тогда в конце первого года вклад составил 1,2P, а в конце второго года — 1,2²P, в начале третьего года — 1,2³P. В начале четвёртого года — 1,2³P + 1, а в конце — (1,2³P + 1) · 1,2. В начале пятого года — (1,2³P + 1) · 1,2 + 1, а в конце — ((1,2³P + 1) · 1,2 + 1) · 1,2. По условию нужно найти наибольшее целое число P, при котором выполнено неравенство ((1,2³P + 1) · 1,2 + 1) · 1,2 < 8.

Выполнив преобразования, получим:

3888P < 8375, P < 8375 / 3888, P < .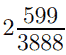

Наибольшее целое решение этого неравенства — число 2. Значит, размер первоначального вклада составляет 200 000 рублей.

Ответ: 200 000 рублей.