Имеется 2500 прямоугольников, у каждого из которых длина и ширина...

Задание:

Имеется 2500 прямоугольников, у каждого из которых длина и ширина выбирается наудачу из отрезка [0, 1] (независимо). По центральной предельной теореме указать симметричные относительно среднего значения границы, в которых с вероятностью 0,99 лежит суммарный периметр всех прямоугольников.

Решение:

Прямоугольники характеризуются двумя своими сторонами:

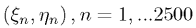
Периметр каждого

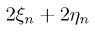
Суммарный периметр

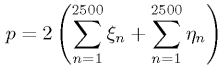
В отличие от задач на объем или площадь, здесь в скобках уже сумма 5000 независимых равномерно распределенных случайных величин Матожидание каждой:

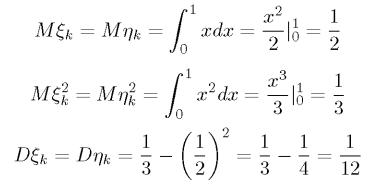
У нас число независимых слагаемых N=5000

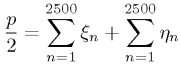
По центральной предельной теореме (ЦПТ):

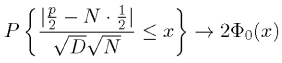
Найдем х, что 2Ф₀(х) = 0, 99. По таблицам х = 2,5758. Интервал характеризуется неравенством

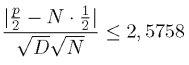
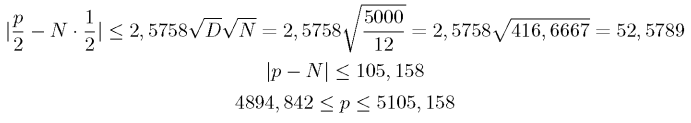
- границы для суммарного периметра