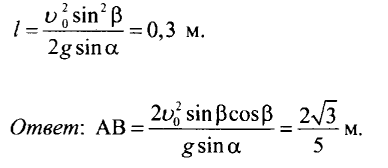Наклонная плоскость пересекается с горизонтальной плоскостью...

Задание:

Наклонная плоскость пересекается с горизонтальной плоскостью по прямой АВ. Угол между плоскостями α = 30°. Маленькая шайба скользит вверх по наклонной плоскости из точки А с начальной скоростью v₀ = 2 м/с, направленной под углом β = 60° к прямой АВ. Найдите максимальное расстояние, на которое шайба удалится от прямой АВ в ходе подъема по наклонной плоскости. Трением между шайбой и наклонной плоскостью пренебречь.

Решение:

Выбор системы координат: ось х направлена по прямой АВ, ось у — вверх по наклонной плоскости перпендикулярно линии АВ (см. рис.).

Проекции вектора ускорения свободного падения :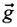

Кинематика движения по наклонной плоскости эквивалентна кинематике движения тела, брошенного под углом β к горизонту, в поле тяжести с ускорением g sin α

Запишем зависимости от времени t для проекций скорости тела и его радиуса-вектора на оси х и у (в известных уравнениях для тела, брошенного под углом β  к горизонту, делается замена g → g sin α):

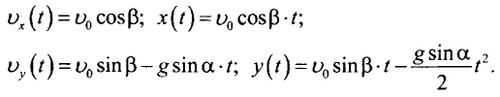
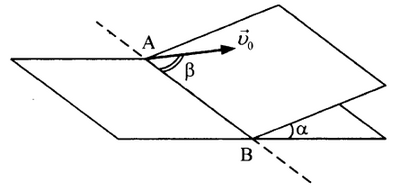
Условие 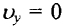 позволяет найти время подъема, а затем максимальное удаление l от прямой АВ на наклонной плоскости: